Arduino

Arduino
un arduino es una compañia de hardware libre y una comunidad tecnologia que diseña y manufactura placas computadoras de desarrollo de hardware y software compuesta respectivamente por circuitos impresos que integran un microcontrolador y un entorno de desarrollo de donde se programa cada placa .
Arduino se enfoca en acercar y facilitar el uso de la electronica y programacion de sistemas enbebidos en proyectos multidisciplinarios de toda la plataforma tanto como para su componente de hardware como de software, son liberados con licencia de codigo abierto que permite la libertad de acceso a ellos .
Esto mas que todo es una placa base que sirve para dar soporte a los dispositivos ya sean en robots u objetos .

Impresoras 3D

La impresora 3D es aquella que permite crear o imprimir aquellas piezas que conforman un dispositivo de arduino cada pieza tarda de media hora a hasta 3 horas dependiendo del tamaño primeramente esta conformada por una placa base que sirve de soporte y funcionamineto de esta, se encuntra compuesta por sensores y motores asi dandole potencia y los pulsos segun lo programado de la pieza .

Alumno y estudiante

Diferencia entre alumno y estudiante 

Un estudiante es una persona que estudia independientemente de si y es autodidacta o si tiene un profesor,mirntras que un alumno es un discipulo respecto a su maestro de la materia que esta aprendiendo algo de la escuela colegio o universidad que necesita un guia.

Relaciones

Tema  #3                             Relaciones 

se habla de relación cuando dos objetos tienen relación entre ellos, en geometría se trata de relaciones de congruencia y de semejanza; en áljebra,de relaciones de igualdad o desigualdad numérica; en teoría de conjuntos, de relaciones de pertenencia y de inclusión. por esto, es necesario formular la noción general de relaciones entre objetos.

R es una relación de A en B ↔ p⊂AxB

Ejemplo:

sea A={1,2,3}
      B={a,b,c}
      R1,R2,R3 de AxB
      AxB={(1,a),(1,b),(1,c),(2,a),(2,c),(3,a),(3,b),(3,c)}
      R1={(1,a)}
      R2={(1,b),(1,c)}
      R3={(2,b),(3,b),(3,c)}

_Dominio,Imagen y Relación inversa

si R es un subconjunto del producto cartesiano AxB, es una relacion de A en B, existen dos importantes conjuntos asociados de esta relación dominio e imagen de R

_Dominio

el dominio de R que se escribe D(R) es el conjunto de los elementos de A que están relacionados con algún elemento del conjunto, en otras palabras el dominio de R es un subconjunto de A y es el conjunto de todos los primeros elementos de los pares ordenados que pertenecen a R, es decir:

D(R)= {x/(x,y)∊ R}

_Imagen

(rango o recorrido de R) que se escribe I(R) es el conjunto de los elementos de B que son los segundos elementos de dos pares ordenados x,y que pertenecen a R en otras palabras es todo los elementos de B que están relacionados con todos los elementos de A

I(R)= {y,(x,y)єR}

_Relación inversa

en la relación de R,A y B es la relación de R´ de B en A se detienen de R´ {(y,x)/(x,y)∈R

_Composición de relaciones 

sea R una relación de A en B y S una relación de B en C

R⊂(AxB) S⊂BxC

la composición de una relación se puede definir de A en C como composición de R y S mediante:

SoR={(x,z)/∃y∈BΛ(x,y)∊R∧(y,z)∈S}

(x,z)∊SoR↔∃y∈B∧(x,y)∈R∧(y,z)∊S}


_Propiedades Relación inversa de una composición

(SoR)´=R´oS´

_Definición de composición 

(SoR)(x)=S[R(X)]

(1,2)=S[R(1)]=S(2)=∌

_Relación definidas de un conjunto

AxA=A²

R⊂AxA

_Relaciones en RxR (plano cartesiano)

R,⊂RxR

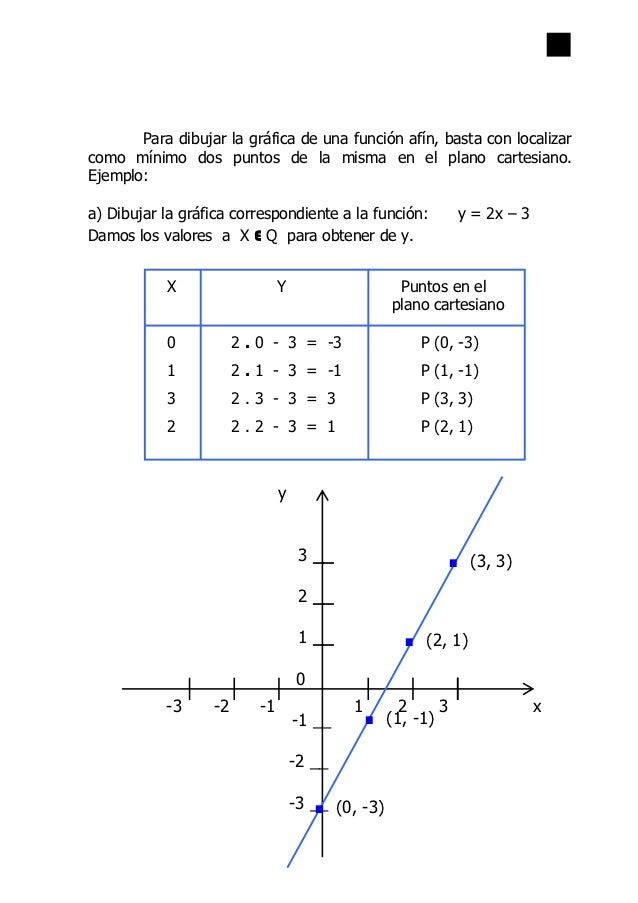
sea R una relación definida en A estas relaciones generalmente satisfacen ciertas propiedades que pondremos a continuación:

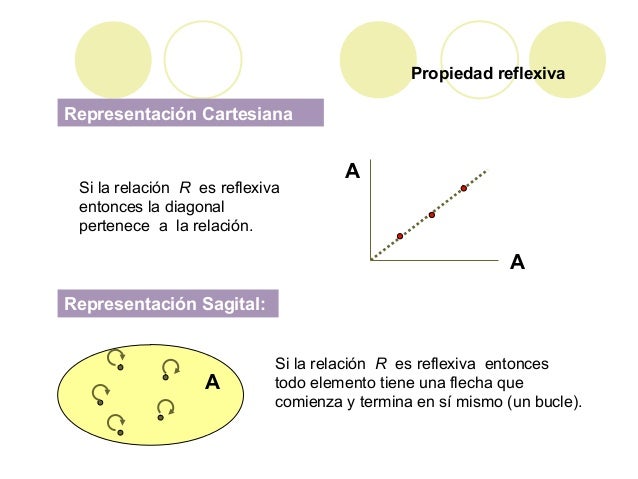
_Relaciones reflexivas 

una relación R definido en un conjunto A se denomina reflexiva si cada elemento x del conjunto A esta relacionado consigo mismo 

 sea R⊂A² / (x,y)∈xRy

R es reflexiva ↔∀x,∊A⇾xRy



_Relaciones simetricas

una relación en un conjunto A es simétrica si cualquiera que sea el par ordenado (x,y) que pertenece a la relación entonces el par ordenado (y,x) también pertenece a la relación

R es simetrica ↔ ∀x,∀y∊A,xRy ➝yRx




_Relaciones transitivas

una relación R definido en un conjunto A es transitiva si cualquiera que sean los pares ordenado (x,y) y (y,z) que pertenecen a las relación entonces el par ordenado (x,z) también pertenece a la relación

∀x,∀y,∀z: xRy∧yRz￫xRz


_Relaciones de equivalencia

una relación R en un conjunto A es de equivalencia sin es reflexiva, simétrica y transitiva. En otras palabras si cumple las anteriores 3 mencionadas.

Conjuntos

Tema  #2                                                   CONJUNTOS 

Empleamos el vocablo de conjuntos para referirnos a un objeto que se encuentra agrupado formando un todo, de esta noción de pluralidad contrapuesta a la singularidad ha sugerido el concepto matemático de conjunto.

para poder expresar los elementos que pertenecen a un conjunto se emplean las letras minúsculas a,b,c, y para denotar a los conjuntos las letras mayúsculas:

"/" para expresar " tal que "

"∈" pertenece a un conjunto

"<" para expresar menor que

">"para expresar mayor que 

キ diferente 

_Notación de conjuntos 

Naturales N= {1,2,3....}

Enteros  Z={....-2,-1,0,1,2,3}

Racionales Q={2,0,5,2/3,0,6}

Irracionales Q´={ㅠ,√2,....}

Reales R= NUZUQUQ´

Imaginario ㅍ{i,0,√-b....}

Complejos C=  RUㅍ

_Diagrama de Venn

_Diagrama de un conjunto 

los conjuntos se pueden determinar de dos maneras:

Por extensión:                                                                                                                                

se dice que un conjunto esta 

determinado por extensión 

si y solamente si se nombra 

a todos los elementos que 

constituyen dicho conjunto 

(se escribe todos los 

elementos del conjunto)

Ejemplo:

A={1,2,3,4,5}

B={a,e,i,o,u}

C={a,e,o}

Por comprensión:

un conjunto esta determinado 

por comprensión cuando existe

 una propiedad que caracteriza 

a todos los elementos de un 

conjunto

Ejemplo:

A={x∊N/x<6}

B={x/x es vocal}

C={x/x es vocal fuerte}

Ejemplos:

Por extensión= {a,b,c,d,e,f,g,h,i,j,k,l,m,n,ñ,o,p,q,r,s,t,u,v,w,x,y,z}
Por comprensión= {letras del abecedario} 
 
Por extensión= {lunes,martes,miércoles,jueves,viernes,sábado,domingo}
Por comprensión= {días de la semana} 

Por extensión= {do,re,mi,fa,sol,la,si} 
Por comprensión= {notas musicales} 

Por extensión= {0,1,2,3,4,5,6,7,8,9} 
Por comprensión= {digitos} 

Por extensión 
{enero,febrero,marzo,abril,mayo,junio,... }
Por comprensión= {meses del año }

_Conjuntos especiales

se llaman conjuntos especiales aquellos conjuntos que se caracterizan por el numero de elementos que compone dicho conjunto: conjunto unitario,vacio,universal.

1)conjunto unitario: 

es aquel conjunto que se caracteriza por tener un solo elemento

Ejemplo:

A={x∊N/х2-4=0}={2}

B={x∈Z/x3=0}={0}

_Conjunto Vacio

es aquel conjunto que se caracteriza por no tener elementos 

A={x⋲N/x2+5x+6=0}={}

B={x⋲R/x2+4=0}={}

_Conjunto universal

es un conjunto del que a partir de un elemento se puede formar otro subconjunto

Ejemplo:

U={x∊N/x<10}={1,2,3,4,5,6,7,8,9}

A={x∊U/2x2-5x+3=0}={1}

B={x∊U/x es primo}={1,2,3,4,5}

Relación de conjuntos

_Inclusión de conjuntos

sea A y B dos conjuntos de un mismo universo. se dice que A está incluido en B, o que A,es un subconjunto de B, si todos los elementos del conjunto A pertenecen al conjunto B; se denota por A⊂B, que se lee " A esta incluido en B" o bien "B esta incluido en A" o bien " A es un subconjunto de B"

En símbolos

A⊂B⇿ұx:x∊A⇾x∊B

_Igualdad de conjuntos

se dice que A y B no son iguales si A es un conjunto de B y B es un conjunto de A es decir; si ambos conjuntos estan formadas por los mismos elementos

A=B↔ A⊂B ∧ B⊂A

_Conjuntos de partes

se entiende por conjunto por parte de A el conjunto formado por todos lo0s subconjuntos de A, y se denota por: p(a)

Operaciones entre conjuntos 

_Unión de conjuntos

dados dos conjuntos de A y B, se llama unión de A y B, al conjunto formado por todos los elementos de A o de B. se denota por AUB.

En símbolos

AUB={x/x∊A ν x∊B}

Es decir

x∊(AUB) ↔ x∊A ν x∊B

_Intersección de conjunto

sean A y B dos conjuntos definidos en un universo se llama intersección de A y B al conjunto formado por los elementos que pertenecen al conjunto de A y al conjuntos de B 

En símbolos 

A⋂B={x/x∊A ៱ x∊B}

x∊(A៱B)↔ x∊A៱ A∊B

_Complemento de un conjunto

sea A un conjunto definido en un universo U el complemento de A es el conjunto formado por todos los elementos de U que no pertenecen al conjunto  A

En símbolos 

_Diferencia de conjuntos

sean dos conjuntos de A y B definidos en un universo la diferencia de conjuntos de A-B es el conjunto formado por todos los elementos de A que no pertenecen a B

En símbolos

A-B

A-B={x/x∈A∧x∉B}

_Diferencia simétrica de un conjunto

sean dos conjuntos definidos en un universo la diferencia simétrica entre dos conjuntos es el conjunto formado por los elementos formados que pertenecen al conjunto A y B, pero no a ambos conjuntos. se denota por :

En símbolos

A∆B=(A-B)U(B-A)

 A-B=(A∩B^∁ )U(B∩A^∁)

_Cardinalidad de conjuntos

sea A un conjunto finito en un universo U llamamos cardinalidad el número de elementos del conjunto A y se denota por: n(a)

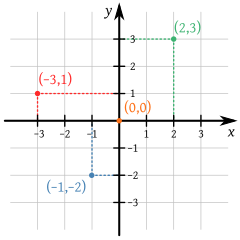
_Producto cartesiano

el producto cartesiano de los conjuntos A y B es el conjunto cuyos elementos son todos los pares ordenados (x,y) donde la primera componente pertenece al conjunto A y la segunda componente pertenece a B

En símbolos 

AxB={(x,y)/x∈A៱ y∈B}

Números Amigos

Números Amigos

Dos números amigos son dos números enteros positivos a y b tales que la suma de los divisores propios de uno es igual al otro número y viceversa, es decir σ(a)=b y σ(b)=a, donde σ(n) es igual a la suma de los divisores de n, sin incluir a n. (La unidad se considera divisor propio, pero no lo es el mismo número.).

Un ejemplo es el par de naturales (220, 284), ya que:

• los divisores propios de 220 son 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 y 110, que suman 284;
• los divisores propios de 284 son 1, 2, 4, 71 y 142, que suman 220.

Si un número es amigo de sí mismo (es igual a la suma de sus divisores propios), recibe entonces el nombre de número perfecto.

Número Capicúa

Número Capicúa

La palabra capicúa (del catalán cap i cua, «cabeza y cola») (en matemáticas, número palindromo) se refiere a cualquier número que se lee igual de izquierda a derecha que derecha a izquierda. Ejemplos: 161, 2992, 3003, 2882,22.

Números Primos

Números primos

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499.