Relaciones

Tema  #3                             Relaciones 

se habla de relación cuando dos objetos tienen relación entre ellos, en geometría se trata de relaciones de congruencia y de semejanza; en áljebra,de relaciones de igualdad o desigualdad numérica; en teoría de conjuntos, de relaciones de pertenencia y de inclusión. por esto, es necesario formular la noción general de relaciones entre objetos.

R es una relación de A en B ↔ p⊂AxB

Ejemplo:

sea A={1,2,3}
      B={a,b,c}
      R1,R2,R3 de AxB
      AxB={(1,a),(1,b),(1,c),(2,a),(2,c),(3,a),(3,b),(3,c)}
      R1={(1,a)}
      R2={(1,b),(1,c)}
      R3={(2,b),(3,b),(3,c)}

_Dominio,Imagen y Relación inversa

si R es un subconjunto del producto cartesiano AxB, es una relacion de A en B, existen dos importantes conjuntos asociados de esta relación dominio e imagen de R

_Dominio

el dominio de R que se escribe D(R) es el conjunto de los elementos de A que están relacionados con algún elemento del conjunto, en otras palabras el dominio de R es un subconjunto de A y es el conjunto de todos los primeros elementos de los pares ordenados que pertenecen a R, es decir:

D(R)= {x/(x,y)∊ R}

_Imagen

(rango o recorrido de R) que se escribe I(R) es el conjunto de los elementos de B que son los segundos elementos de dos pares ordenados x,y que pertenecen a R en otras palabras es todo los elementos de B que están relacionados con todos los elementos de A

I(R)= {y,(x,y)єR}

_Relación inversa

en la relación de R,A y B es la relación de R´ de B en A se detienen de R´ {(y,x)/(x,y)∈R

_Composición de relaciones 

sea R una relación de A en B y S una relación de B en C

R⊂(AxB) S⊂BxC

la composición de una relación se puede definir de A en C como composición de R y S mediante:

SoR={(x,z)/∃y∈BΛ(x,y)∊R∧(y,z)∈S}

(x,z)∊SoR↔∃y∈B∧(x,y)∈R∧(y,z)∊S}


_Propiedades Relación inversa de una composición

(SoR)´=R´oS´

_Definición de composición 

(SoR)(x)=S[R(X)]

(1,2)=S[R(1)]=S(2)=∌

_Relación definidas de un conjunto

AxA=A²

R⊂AxA

_Relaciones en RxR (plano cartesiano)

R,⊂RxR

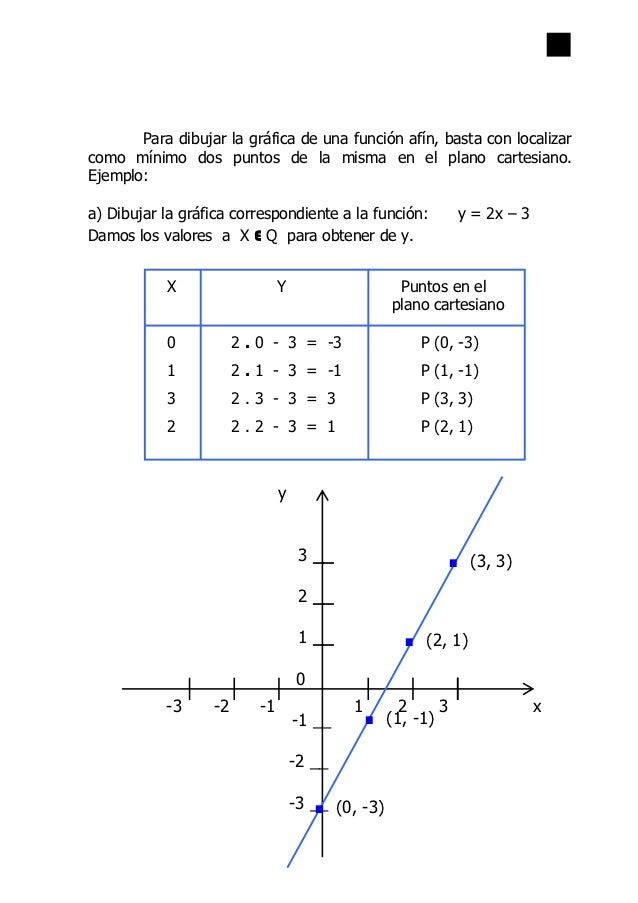
sea R una relación definida en A estas relaciones generalmente satisfacen ciertas propiedades que pondremos a continuación:

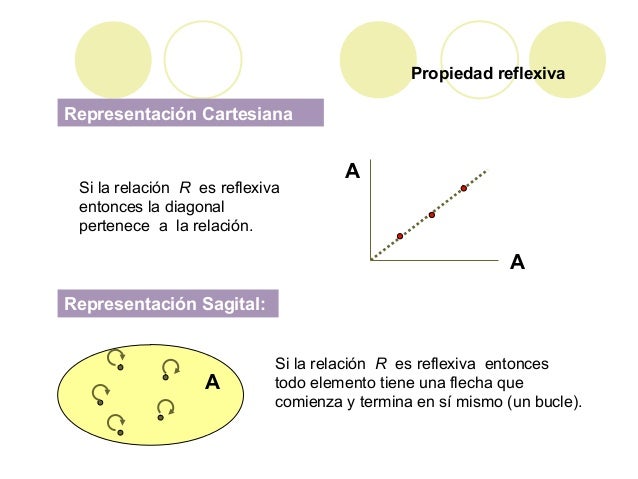
_Relaciones reflexivas 

una relación R definido en un conjunto A se denomina reflexiva si cada elemento x del conjunto A esta relacionado consigo mismo 

 sea R⊂A² / (x,y)∈xRy

R es reflexiva ↔∀x,∊A⇾xRy



_Relaciones simetricas

una relación en un conjunto A es simétrica si cualquiera que sea el par ordenado (x,y) que pertenece a la relación entonces el par ordenado (y,x) también pertenece a la relación

R es simetrica ↔ ∀x,∀y∊A,xRy ➝yRx




_Relaciones transitivas

una relación R definido en un conjunto A es transitiva si cualquiera que sean los pares ordenado (x,y) y (y,z) que pertenecen a las relación entonces el par ordenado (x,z) también pertenece a la relación

∀x,∀y,∀z: xRy∧yRz￫xRz


_Relaciones de equivalencia

una relación R en un conjunto A es de equivalencia sin es reflexiva, simétrica y transitiva. En otras palabras si cumple las anteriores 3 mencionadas.