Tema #1
_Lógica
Es la disciplina encargada de ver los diferentes tipos de razonamientos que ofrece diferentes formas de leyes para determinar si es V o F.
Una de las metas fundamentales de la lógica es eliminar la Ambigüedad de un lenguaje ordinario, introduciendo simbolos y conectivos lógicos en la constitución de posiciones. dado que las proposiciones son la base del razonamiento lógico que consiste en decidir la validez de una idea en base a un enunciado que previamente fueron aceptados.
Ambigüedad---> Algo que tienen doble sentido
_Objetivo de la lógica
-lenguaje claro y preciso
-razonamientos correctos
_Proposiciones
Es toda oración o enunciado respecto del cual se puede definir si es verdadero o falso pero no ambos a la vez,Es decir toda proposición esta asociada a un valor de verdad lo cual puede ser verdadero o falso.
Así una proposición es verdadera si se dice que su valor de verdad es V, y es falso si su valor de verdad es F.
_Nota:
una proposición es una oración que tiene un solo valor de verdad en el transcurso del tiempo, o cualquiera sea el lugar de donde se este utilizando dicha proposición.
Ejemplo:
_Los gatos hablan si es proposición
_Mañana sale el sol si es proposición
_Cual es tu nombre no es proposición
_5+4= 8 si es proposición
_El ser humano es el arquitecto de su propio destino si es proposición
_El sol es cuadrado si es proposición
_Que hora es no es proposición
_Que belleza! no es proposcisión
_Los perros ladran si es proposición
_conectivos lógicos
A las proposiciones simples o genéricas (atómicas) se acostumbran denotar por las letras p,q,r....
Ejemplo:
p: "Los gatos hablan" F
~p: V
q:"la tierra es esférica" V
~q: F
A partir de proposiciones simples se pueden generar otras proposiciones simples o compuestas utilizando ciertas constantes proposicionales llamados conectivos lógicos tales como el conectivo no.
no, en símbolo "~"
y, en símbolo "∧"
o, en símbolo "V"
si entonces, "➞"
si solo si, "⟷"
o excluyente, "⊻"
_Operaciones proposicionales
Dada una o dos proposiciones cuyo valor de verdad se conoce,las operaciones entre proposiciones tratan de generar otras proposiciones y caracterizar la proposición resultante a través de su valor de verdad, estas son la negación,conjunción,disyunción,implicación ,doble implicación y disyunción excluyente.
_Negación
Sea una proposición p se llama negación de p a la proposición que se obtiene uniendo el conectivo "no". se denota en símbolos por "~p".
_Tabla de verdad
Ejemplo:
p: "Los gatos hablan" F ∼ p: "Los gatos no hablan" V
q: V ∼q:
V ∼q: "≠" F
"≠" F
_Conjunción
se llama conjunción de p y q a la proposición que se obtiene por medio del conectivo y, se escribe "ʌ" .
p
|
ʌ
|
q
|
V
V
F
F
|
V
F
F
F
|
V
F
V
F
|
_Nota:
el valor de verdad de la conjunción es verdadero si ambos valores de verdad son verdaderos, caso contrario es F.
Ejemplo:
p:"juan es orientista"
q:"pedro es orientista"
p∧q:"juan y pedro son orientistas"
_Disyunción
la disyunción de dos proposiciones p y q se llama a la proposición que se obtiene uniendo promedio del conectivo o, se escribe "V".
p
|
V
|
q
|
V
V
F
F
|
V
V
V
F
|
V
F
V
F
|
_Nota:
solo es falso si los dos son falso, caso contrario es verdadero
Ejemplo:
p:"juan es orientista"
q:"juan es bloominista"
pVq: "juan es orientista o bloominista"
_Implicación
Se llama implicaciones de dos proposiciones p y q a la proposición que se obtiene uniendolas por medio del conectivo "si entonces" se escribe p➞q y se lee " si p entonces q", donde p es el antecedente y q el consecuente.
p
|
➞
|
q
|
V
V
F
F
|
V
F
V
V
|
V
F
V
F
|
_Nota:
El valor de verdad de la implicación de p y q es falso si el antecedente es verdadero y el consecuente falso.
_definición de implicación
p➞q ≡ ∽pνq
_Doble Implicación o Bicondicional
Se llama doble implicación o Bicondicional de dos proposiciones p y q a la proposición que se obtiene uniendolas por medio del conectivo "si solo si", se escribe p➞q y se lee " p si solo q".
p
|
↔
|
q
|
V
V
F
F
|
V
F
F
V
|
V
F
V
F
|
_Nota:
el valor de verdad de la doble implicación entre p y q es verdadero si ambos tienen el mismo valor de verdad caso contrario es falso.
_Definición de Doble Implicación
p↔q ≡ (p⇢) ∧ (q⇢p)
_Disyunción Exclusiva
se llama disyunción exclusiva de dos proposiciones p y q a las proposiciones que se obtiene uniendolas por el conectivo o excluyente, se escribe "p⊻q", se lee"p excluye a q".
p
|
⊻
|
q
|
V
V
F
F
|
F
V
V
F
|
V
F
V
F
|
_Nota:
el valor de verdad de la disyunción exclusiva entre p y q es verdadera si los valores de verdad son diferentes (opuestos), caso contrario es falso.
_Definición de disyunción excluyente
p ⊻q ≡ ∽(p↔q)
_Formulas proposicionales
una formula proposicional es una combinación de proposiciones y conectivos lógicos que simboliza una proposición compuesta o molecular.
а) [p⇾(q v r)] ↔[(pvq) ៱r]
b) (p⟶q) ⇾r
_Tabla de valores de verdad
el valor de verdad de una formula proposiciónal diferente de los valores de verdad de la proposiciones simples que la componen.
es decir se debe analizar todas las posibles combinaciones de valores de verdad de las proposiciones que la componen las cuales se dan en las primeras columnas, por tanto si en una formula proposicional intervienen "n" proposiciones el numero de proposiciones para la tabla de valor de verdad se calcula con 2 elevado a la "n".
(p⇾q) v (∼pvr)
p ∼p
|
q
|
r
|
(p⇾q)
|
v
|
(∼pvr)
|
|
|
V F
|
V
|
V
|
V
|
V
|
V
|
V F
|
V
|
F
|
V
|
V
|
F
|
V F
|
F
|
V
|
F
|
V
|
V
|
V F
|
F
|
F
|
F
|
F
|
F
|
F V
|
V
|
V
|
V
|
V
|
V
|
F V
|
V
|
F
|
V
|
V
|
V
|
F V
|
F
|
V
|
V
|
V
|
V
|
F V
|
F
|
F
|
V
|
V
|
V
|
|
_Clasificación de formulas proposicionales
las formulas proposicionales se clasifican según el valor de verdad de su columna resultante como : tautología, contradicción y contingencia.
_Tautoligía
es una formula proposicional verdadera para cualquier proposición entrada de dicha formula proposicional.
_Contradicción
es una formula proposicional que es falso para cualquier combinación de entrada de dicha formula proposicional
_Contingencia
es una formula proposicional que no es tautologia ni contradicción
_Equivalencias lógicas
dos formulas proposicionales son lógicamente equivalente si su tabla de verdad se expresan de la misma forma
(p⇾q)≡(∼p∨q)
p
|
q
|
p⇾q
|
∼p
|
∼p∨q)
|
V
V
F
F
|
V
F
V
F
|
V
F
V
V
|
F
F
V
V
|
V
F
V
V
|
SON EQUIVALENTES
_Aljebra de Proposiciones
son operaciones lógicas que se realiza mediante proposiciones aplicando ciertas tablas básica llamadas leyes lógicas. Es decir como en aljebra básica donde la simplificación de expresiones aljebraicas es muy importante en lógica también existe la necesidad de simplificar formulas proposicionales complejas a través de ciertas equivalencias llamadas leyes lógicas.

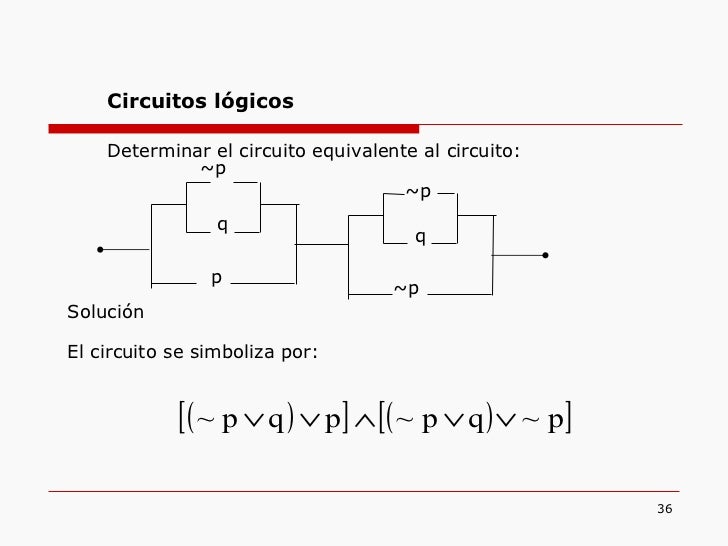
 _Circuitos lógicos
_Circuitos lógicos
un circuito con interruptor puede estar abierto o cerrado cuando el interruptor esta abierto no permite el paso de corriente mientras que cuando esta cerrado si lo permite, si asociamos una proposición a cada interruptor, intuitivamente vemos en el aljebra de circuitos la V (verdad), de tal proposición indica que esta cerrado y F(falso), si esta abierto.

 _Reglas de inferencia
_Reglas de inferencia
se debe entender por inferencia lógica a un razonamiento en el que a partir de un conjunto de proposiciones llamadas premisas se obtiene un resultado llamado conclusión. un razonamiento es válido sí, y solamente sí, la conjunción de las premisas implica la conclusión, o la conclusión es consecuencia de las premisas. Es decir, si las premisas son todas verdaderas, entonces las conclusiones que se derivan de ellas lógicamente han de ser verdaderas,sin embargo,si una o más de las premisas es falsa,la conjunción de todas las premisas es falsa, por tanto, la conclusión puede ser verdadera o falsa.
_Tabla de Reglas de Inferencia
_Ejemplos